Maurits Cornelis Escher (1898-1972) was born in the Netherlands and, at first, wanted to be an architect.

That's what he studied before transferring to the decorative arts. Soon enough he moved to Rome, leaving in 1935 and returning via Switzerland and Belgium to his homeland.

Escher's artistic career was, until the last years of his life, one of relative obscurity; now his work is some of the most famous in the world.

He's often described as a "graphic artist", which sounds like a modern idea. But Escher's style was, in truth, an old one...

For Escher's main medium was woodcut - where a picture is engraved into a wooden block which is then covered with ink and used for making prints.

Woodcuts had been popular in Europe since the 1400s; Albrecht Dürer (1471-1528) was one of the early masters of this form:

By their very nature woodcuts are better suited to minute detailing than painting; they have a certain precision which paint struggles to match, being made up of lines rather than colours.

Gustave Doré, who lived in the 19th century, was another master of the medium:

Perhaps Escher's most direct forebear was the etcher Giambattista Piranesi (1720-1778), who created a series of "Imaginary Prisons" in the 1740s.

These dark architectural fantasies bear more than a passing resemblance to Escher's work.

You can see how the woodcut method lent itself to Escher's mathemetical visions, for it permitted exquisite, precise, highly geometric detail.

Escher's personal interests had found their perfect outlet. Consider Metamorphosis III, from 1968:

Escher also produced many lithographs, a printing method which relies on the inability of oil and water to mix, and mezzotints, which use copper plates.

Again, both have significant heritage, and both lend themselves to particular visual forms:

So that was the long tradition of artistic methods on which M.C. Escher drew. But what about the things he actually depicted?

He was clearly fascinated by perspective and by mathematics, by the laws of reality and by the visualisation of the impossible:

Mathematical curiosity in art was not new.

Ever since the work of Giotto in the 1300s and all throughout the subsequent Renaissance, polymathic artists-turned-scientists like Leonardo and Alberti dedicated themselves to understanding the rules of perspective.

Paolo Uccello (1397-1475) was famously obssessed by vanishing point; he would stay up for nights on end, refusing to work on anything else or leave his house until he had discovered its rules.

The Hunt in the Forest (1470) is a perspectival experiment as much as a painting:

And it was such experimentation that allowed for the creation of frescoes in Renaissance churches, where flat walls and domes were given depth.

Any appearance of depth on a flat surface is, technically, an optical illusion. In this way, Escher doesn't seem so unusual.

Escher's fascination with spherical mirrors was not without precedent either. Parmigianino made his own self-portrait in a convex mirror in 1524, and Jan van Eyck's Arnolfini Portrait from 1436 features the most famous convex mirror in all of art:

But these artists had been interested in portraying the world as it really appears; their experiments with perspective were about capturing reality according to its observable rules.

Escher lived in a totally different age, culturally and artistically and scientifically...

The Post-Impressionists, who had moved away from representational art, were followed by the Surrealists and the Cubists and, eventually, a full embrace of Abstract Art.

Painters like Picasso and Dali weren't interested in reality as we perceive it - they played with its rules:

Even though he never met any of these artists, it was in this broad context that Escher worked, and he followed the Surrealist route of Dali and Magritte by creating pictures which lay in the uncanny valley.

A familiar world, but one with different laws of nature:

Escher's art is unashamedly intellectual - it provokes the mind rather than stirring the heart; such was the atmosphere of much 20th century art.

And yet Relativity, from 1953, captures the imagination with its striking, almost unnerving reworking of reality as we know it:

And, as in Waterfall (1961), there's a certain joy in the precision of Escher's strange realities, a delight in exploring this bizarre, impossible world.

He was clearly a master of the art of printmaking, one who deserves to be considered alongside Duerer and the rest.

And the spirit of post-war Europe, devastated by the darkness and doom of totalitarianism, is reflected in his work.

After all, Escher left Italy because of the rise of Fascism, and in Ascending and Descending (1960), the identical hooded figures speak to such anxieties.

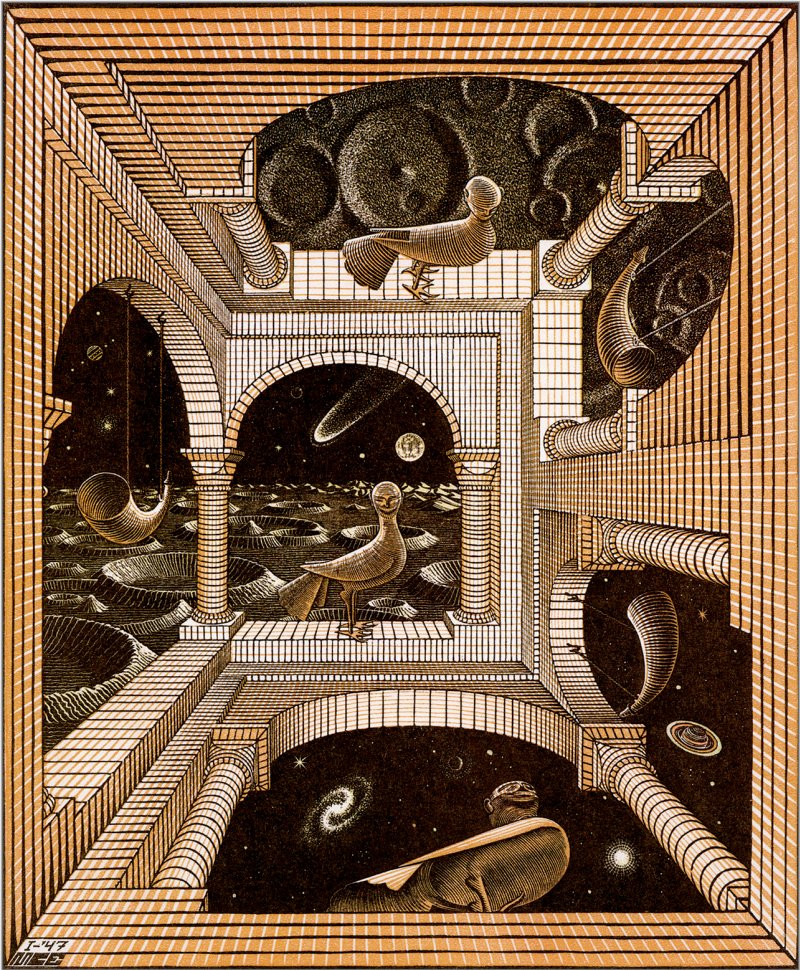
In Another World (1947) we see Escher again playing with the laws of physics and of gravity - a thoroughly 20th century work of art, as human science and technology achieved much previously unimaginable.

That being said, one of Escher's biggest inspirations was a trip to Spain in the 1920s, where the abstract, geometric art of Moorish architecture - as in the 14th century Alhambra - made him realise the possibilities of mathematical art.

But some of Escher's greatest works are neither his impossible mathematical visions nor his abstract geometric experiments.

In Puddle (1952) and Rippled Surface (1950) Escher creates worlds which, though enduringly surreal, are more contemplative, atmospheric, and mysterious.

In Three Worlds, from 1955, Escher seems to be exploring the different planes of reality which exist even in an ostensibly "normal" scene.

And, as ever, it is gloriously and beautiful realised; Escher's style, balanced between simplicity and complexity, exceeds any context.

In Three Spheres (II), from 1946, there are multiple realities at play again.

The three spheres are like three different worlds, and reflected in the central one we see the other two, Escher himself, and Escher making this very image, recurring infinitely...